受験対策で使われる偏差値とは？定義・計算方法・具体例を解説！
こんにちは、鈴木俊吾（すずしん）です。
学生時代では、受験対策をすることになりますよね？
その際、考慮する項目の一つに『偏差値』があります。
志望校選びの目安として、偏差値を基準にする人も多いでしょう。
ところで、この偏差値。
具体的に定義や計算方法を理解しているでしょうか？
何となくニュアンスは分かるけど、詳細までは分からないではないでしょうか？
この記事を読んでいるということは、おそらくあなたも詳しくは知らないですよね。
そこで、今回の記事では、偏差値の定義・計算方法・具体例について解説してみようと思います。
この記事を読めば、偏差値の仕組みがひととおり理解できるようになりますよ。
偏差値とは何か？
『偏差値』というのは、「ある得点が特定の集団内でどの位置にあるか」を表す指標です。
平均を50として、1標準偏差（スケール）を10に標準化したときの値を表します。
受験対策に際し、偏差値を使うことで、以下のことにおいて強みがあります。
偏差値では、50が全体の平均となります。
60になると全体の上位約16%、40になると全体の下位約16%に位置します。
ちなみに、これは正規分布を前提としています。
偏差値の計算式
偏差値を計算するには、以下の手順を踏みます。
1. 平均点（μ）を求める
平均点の計算式は以下のようになります。
要するに、各受験者の点数xiをすべて加算して、受験者数Nで割ることで求められます。
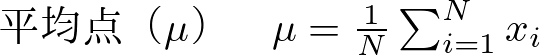
2. 標準偏差（σ）を求める
標準偏差の計算式は以下のようになります。
各受験者の点数xiから平均点μを引いて2乗したものの和をNで割った平方根です。
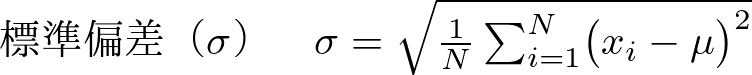
3. 偏差値を計算する
偏差値の計算式は以下のようになります。
計算したい受験者の点数xiから平均点μを引いて、それを標準偏差σで割った値に10を掛けます。
そして、そこから50を足した値になります。
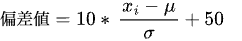
偏差値計算の具体例
例えば、ある科目の受験者が5人いて、それぞれの点数が以下のようになったとします。
| 受験者 | 点数 |
|---|---|
| A | 70 |
| B | 60 |
| C | 80 |
| D | 50 |
| E | 40 |
・平均点（μ）
μ = (70 + 60 + 80 + 50 + 40) / 5 = 300 / 5 = 60
・標準偏差（σ）
差の二乗合計：(10^2+0^2+20^2+(−10)^2+(−20)^2) = 100+0+400+100+400 = 1,000
σ = √(1000 / 5) = √200 ≒ 14.14
・各受験者の偏差値（ここでは例としてAとEを計算してみます）
A = 10 * (70 – 60) / 14.14 + 50 ≒ 57.1
E = 10 * (40 – 60) / 14.14 + 50 ≒ 35.9
偏差値を活かすコツ
偏差値を計算したり確認したりすることで、自分がその科目を得意・不得意なのかを客観的に把握しやすくなります。
あなたが志望する学校の偏差値に達しているかどうかの参考にしてくださいね。
まとめ：偏差値の計算式の意味を理解すればバッチリ！
今回の記事では、偏差値の定義・計算方法・具体例について解説してみました。
一見、計算式が難しそうに思えるかもしれませんが…。
それぞれの計算式の意味を考えながら読んでみると、比較的理解しやすいかと思います。
あなたは、志望校の偏差値に届いているでしょうか？
もし現時点で届いていなくても大丈夫。
これから受験対策をしっかりとしていけば、必ず偏差値は上がっていきますよ。
正しい勉強をすることで、合格水準まで到達することも十分可能なはずです。
これまでの努力は必ずあなたの力となります。
どんなに小さな一歩でも、その積み重ねが確かな自信へとつながるのです。
模試の結果が思うように出なくても、焦らず振り返りと改善を重ねれば必ず成長できます。
つまずいたときは、立ち止まって深呼吸をし、次にできる最善の一手を考えてみてください。
あなたには「ここまで頑張ってきた自分」がいます。
そしてこれからも「もっとできる自分」へと変わっていく可能性があります。
合格のゴールはもうすぐそこ。
自分を信じて、最後まであきらめずに走り抜けましょう。
あなたなら必ず、志望校の扉を開くことができます！
応援しています。
頑張ってくださいね！
大学卒業後、公務員浪人。何度か挑戦するも失敗。無職8年の後、一念発起してフリーランスに転向。現在は、人生攻略ハンターとして、ブログ・note・Kindle・アプリ開発・作曲・投資などといった、様々なコンテンツを制作しています。Kindle／note／ブログ／アプリの全てで0→1を達成。現状、最高月収は5ケタだけど、本気で「未来の1億円プレイヤー」を狙っています。ちなみにXのフォロワーは2,900人。ここから爆伸び予定。今のうちにフォローしておくとレベルアップの過程が分かります。
【スキルレベル】人生攻略ハンターLv5。ブログ Lv5/note Lv4/Kindle Lv4/アプリ Lv5/作曲 Lv0/投資 Lv5。
【装備】MacBook Air M4/iPhone 12/POCO X7 Pro/Anker SoundCore 2/ポロシャツ/ハーフパンツ。
【資格】3級ファイナンシャル・プランニング技能士/WEBライター検定3級/.com Master BASIC/ネットマーケティング検定（予定）/ダイエット検定2級/実用英語技能検定準2級など。計17種保有。
